Codeforces Round 797 (Div. 3)
A. Print a Pedestal (Codeforces logo?)
题目解析
如果 能够被 整除,我们就可以构造一个高度为 的领奖台。且 。
如果 除以 的余数不为 ,那么我们就从高到低把领奖台高度 ,这样就仍然保持了领奖台单调性。
参考代码
int main() {
int t;
cin >> t;
while(t--){
int n;
cin >> n;
int avg = (n - 6) / 3;
int x1 = 3, x2 = 2, x3 = 1;
int delta = n - 6 - avg * 3;
if(delta == 2) x1++, x2++;
else if(delta == 1) x1++;
x1+= avg, x2 += avg, x3 += avg;
cout << x2 << " " << x1 << " " << x3 << endl;
}
return 0;
}B. Array Decrements
题目解析
要求 数组转化到 数组。
首先确保对于所有的 ,均满足 。
设定需要执行的操作次数是 ,那么 需要满足以下两个条件:
- 如果 ,那么 。
- 如果 ,那么 。
参考代码
int main() {
fastIO();
int t;
cin >> t;
while(t--){
int n;
cin >> n;
vector<int> arr(n), brr(n);
for(auto& it: arr) cin >> it;
for(auto& it: brr) cin >> it;
int delta = inf;
bool ok = true;
int mx = 0;
for(int i = 0; i < n; ++i){
if(brr[i] == 0){
mx = max(mx, arr[i]);
}else{
int d = arr[i] - brr[i];
if(d >= 0){
if(delta == inf){
delta = d;
}else if(delta != d){
ok = false;
break;
}
}else{
ok = false;
break;
}
}
}
if(delta < mx) ok = false;
cout << (ok ? "YES": "NO") << endl;
}
return 0;
}C. Restoring the Duration of Tasks
题目解析
- 如果 ,那么 的实际开始时间是 的到达时间,即 。
- 如果 ,那么 的实际开始时间是 的结束时间和 的开始时间的最大值,即 。
参考代码
int main() {
fastIO();
int t;
cin >> t;
while(t--){
int n;
cin >> n;
vector<int> srr(n), frr(n);
for(auto& it: srr) cin >> it;
for(auto& it: frr) cin >> it;
vector<int> ans(n);
for(int i = 0; i < n; ++i){
if(i){
ans[i] = frr[i] - max(srr[i], frr[i - 1]);
}else{
ans[i] = frr[i] - srr[i];
}
}
for(auto& it: ans) cout << it << " ";
cout << endl;
}
return 0;
}D. Black and White Stripe
题目解析
统计前缀内 B 字符的数目,然后找到一个长度为 的区间,区间内 B 字符的数目最多。
参考代码
int main() {
fastIO();
int t;
cin >> t;
while(t--){
int n, k;
cin >> n >> k;
string s;
cin >> s;
vector<int> ans(n + 1, 0); // B 字符的前缀数目
for(int i = 0; i < n; ++i){
if(s[i] == 'B'){
ans[i + 1] = ans[i] + 1;
}else{
ans[i + 1] = ans[i];
}
}
int res = inf;
for(int i = k; i <= n; ++i){
int cnt = ans[i] - ans[i - k]; // 区间内 B 字符的数目
res = min(res, k - cnt);
}
cout << res << endl;
}
return 0;
}E. Price Maximization
题目解析
两个物品( , )一起打包的cost是
首先计算所有的 。
剩余的 先处理 之后,需要解决的问题就变成了下面这个:
对于 的任意一个排列, 求 的最大值。显然 的值只能为 或者 。
可以通过贪心来使得 满足 的组数越多越好。
参考代码
int main() {
fastIO();
int t;
cin >> t;
while(t--){
int n, k;
cin >> n >> k;
multiset<int> ms;
ll ans = 0;
vector<int> arr(n);
for(int i = 0; i < n; ++i){
int tv;
cin >> tv;
ans += tv / k;
ms.insert(tv % k);
arr[i] = tv % k;
}
sort(itr(arr));
for(int i = 0; i < n; ++i){
if(ms.count(arr[i])){
ms.extract(arr[i]);
auto pos = ms.lower_bound(k - arr[i]);
if(pos != ms.end()){
++ans;
ms.erase(pos);
}
}
}
cout << ans << endl;
}
return 0;
}F. Shifting String
题目解析
首先计算每个置换环所包含的位置和顺序。
然后暴力处理每个置换环,找到操作之后若干次之后满足当前置换环的状态和初始状态相同的最小的操作次数 。
最后求所有 的最小公倍数。
参考代码
int main() {
fastIO();
int t;
cin >> t;
while(t--){
int n;
cin >> n;
string s;
cin >> s;
vector<int> arr(n);
for(auto& it: arr){
cin >> it;
--it;
}
map<int, vector<int>> mp; //置换环的首位和位置数组
vector<int> vis(n, 0);
for(int i = 0; i < n; ++i){
if(vis[i] == 0){
mp[i] = {i};
vis[i] = 1;
int cur = arr[i];
while(cur != i){
mp[i].push_back(cur);
vis[cur] = 1;
cur = arr[cur];
}
}
}
vector<ll> nex; // 置换环的操作次数
for(auto& [k, vec]: mp){
string tmp;
for(auto& pos: vec){
tmp += s[pos];
}
tmp = tmp + tmp;
int len = vec.size();
for(int i = 1; i < vec.size(); ++i){
if(tmp.substr(i, len) == tmp.substr(0, len)){
len = i;
break;
}
}
nex.push_back(len);
}
ll res = 1;
for(auto& it: nex) res = lcm(res, it);
cout << res << endl;
}
return 0;
}G. Count the Trains
题目解析
一个区间合并和拆分问题。
首先想到了用珂学来解决这道问题。
假设有一组数据 ,如下图所示。
虚线代表实际的速度。
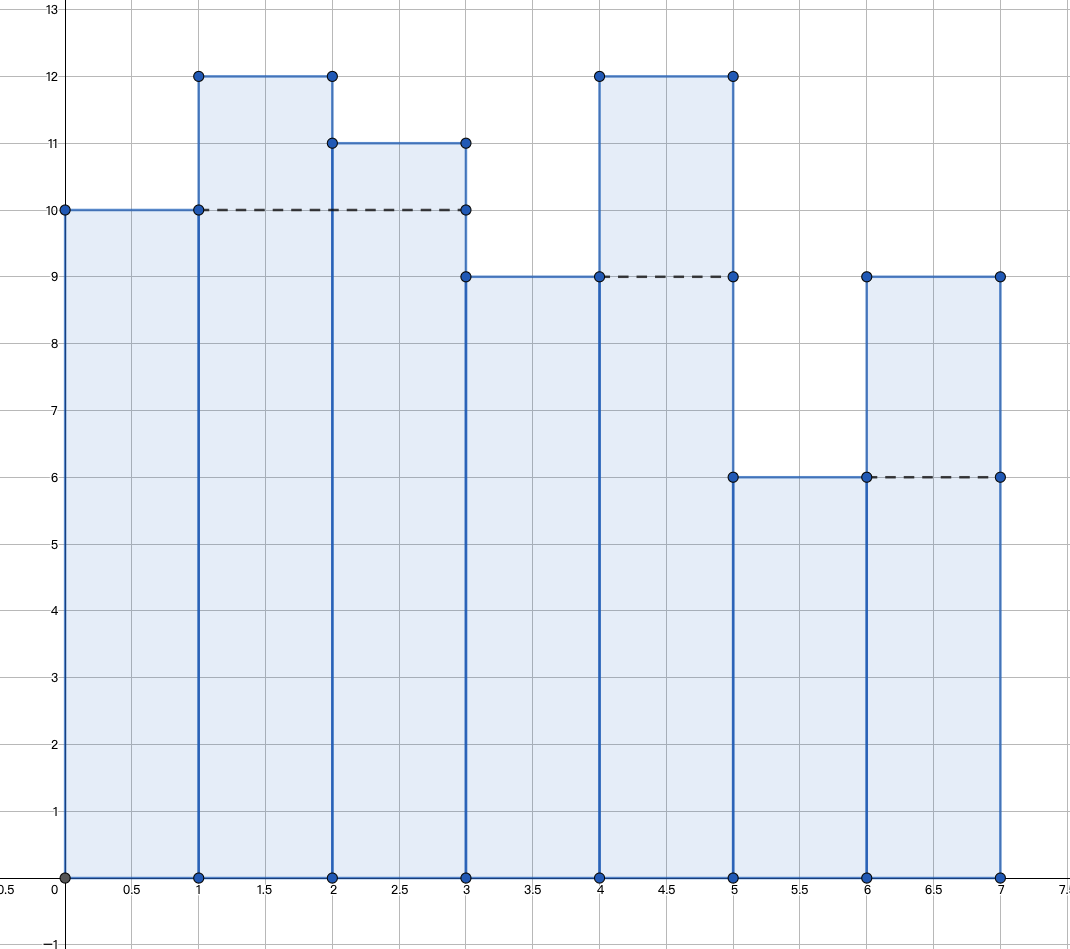
那么速度区间就总共有三个,分别是 ,每个区间的速度等于区间头部的位置的速度。
考虑两种情况,分别用两个独立的case来举例。
一个case是2 1,即将 。
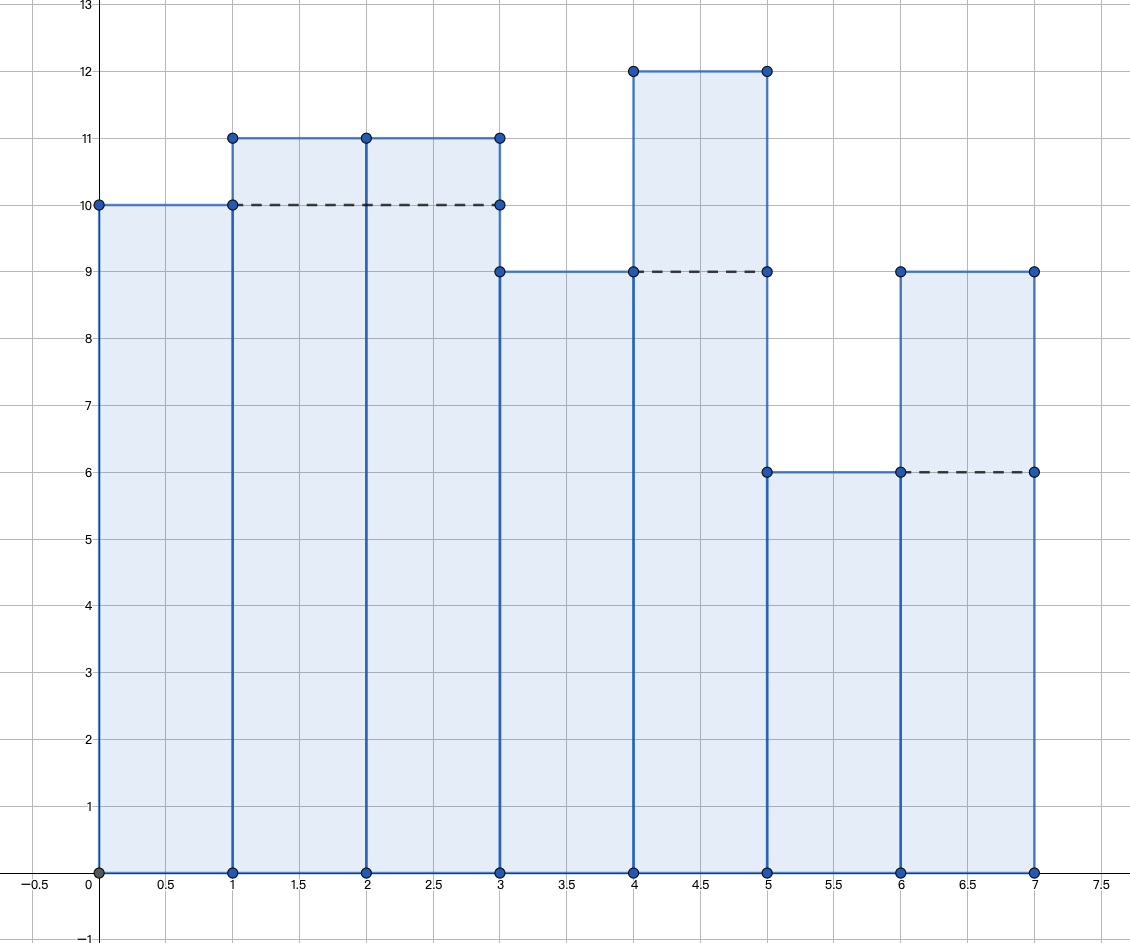
速度区间仍然还是 个,分别是 。
这个case意味着:如果将某个位置速度减小之后,此位置速度仍然不小于它所处的区间的速度的值,那么速度区间不会发生合并和拆分。
另外一个case是 3 3,即 。
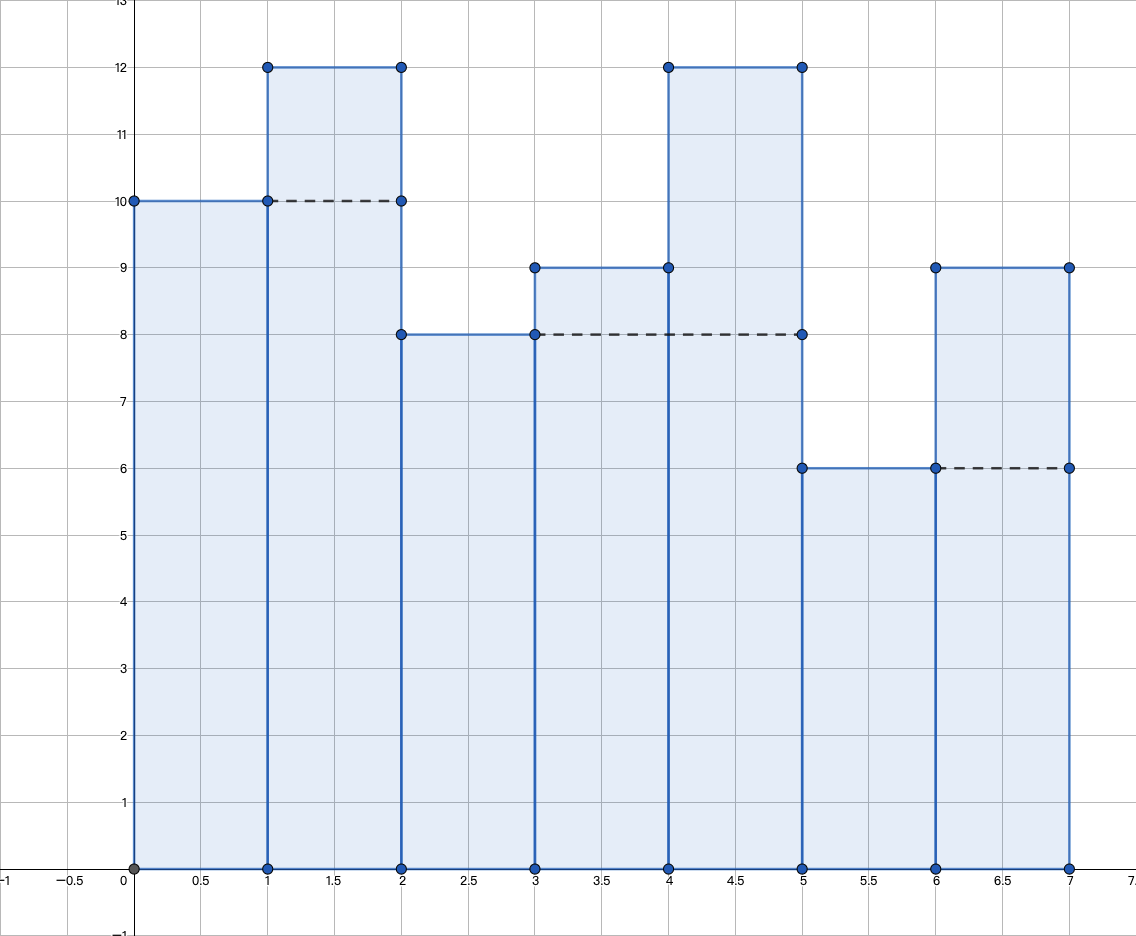
速度区间变成了 个,分别是 。
因为 的速度降低到区间速度以下之后,区间 就拆分成 了。
然后依次比较新的区间和后续区间的速度大小,直到后续无区间或者后续区间速度小于当前区间速度。 区间的速度小于或等于 区间的速度,故可以合并成区间 。 区间速度大于 区间速度,故不合并这两个区间。
这个case代表:如果某个速度减小之后,此位置速度小于它所处的区间的速度,那么速度区间就要进行拆分;如果新区间速度速度不大于后续区间的速度,那么要合并这两个相邻区间,直到后续无区间或者后续区间的速度小于此位置所处的区间的速度。
区间数目即每次查询的结果。
PS: 学过一点珂学,很容易就能想到。
参考代码
int main() {
fastIO();
int t;
cin >> t;
while(t--){
int n, m;
cin >> n >> m;
vector<int> arr(n + 1);
for(int i = 1; i <= n; ++i) cin >> arr[i];
set<PII> st;
int pre = 1;
for(int i = 1; i <= n; ++i){
if(arr[i] < arr[pre]){
st.insert({pre, i - 1});
pre = i;
}
}
st.insert({pre, n});
while(m--){
int k, d;
cin >> k >> d;
auto pos = prev(st.lower_bound({k + 1, k + 1}));
int fv = arr[pos->first];
arr[k] -= d;
if(arr[k] < fv){
PII p = *pos;
st.erase(pos);
if(k > p.first){
st.insert({p.first, k - 1});
}
int nv = p.second;
auto nex = st.lower_bound({k, k});
while(nex != st.end() and arr[nex->first] >= arr[k]){
nv = nex->second;
st.erase(nex);
nex = st.lower_bound({k, k});
}
st.insert({k, nv});
}
cout << st.size() << " ";
}
cout << "\n";
}
return 0;
}